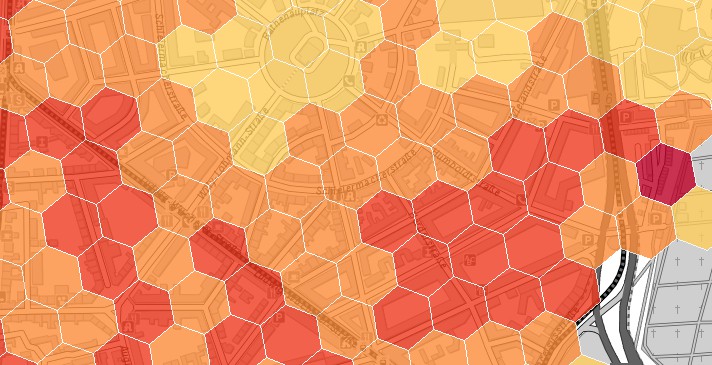
Durch eine Studienarbeit bin ich neugierig geworden: Wie bildet man eigentlich vernüftige statistische Analyseeinheiten? Üblich sind geografische Grenzen (Orts-, Gemeinde, Kreis, Landkreis, …) und quadratische Raster (100 m x 100 m, 1 km x 1km, …). Interessant scheinen aber auch hexagonale Strukturen. Aber warum sollten die besser sein? Was haben sie, was leichter zu generierende Rasterstrukturen nicht haben? Ich wollte es genau wissen (na, manches vielleicht auch nicht sooo genau) und bin fündig geworden:
[1] … Hexagonal Sampling
[2] … Rectangular and hexagonal grids used for observation, experiment and simulation in ecology
Pingback: OGC: Neuer Standard gesucht? | geoObserver
Ich finde die Frage auch recht spannend. Mal gänzlich unmathematisch betrachtet kommen in der Natur hexagonale (oder vernetzte) Muster bei der Bildung flächiger Strukturen vermutlich häufiger vor, als orthogonale, also z.B. Bienenwaben, Schrumpfungsrisse, Leder. Im Sinne einer ganzheitlichen Betrachtung scheint es also nicht abwegig zu vermuten, dass flächenhafte Prozesse und Verteilungen/Ausbreitungen durch diese Elementarzellen „besser“ beschrieben werden können, als durch ein eher künstliches Bezugssystem.
Bei der Modellierung von Ausbreitungsprozessen steht man ja auch stets vor der Frage, mit FEM (also Dreiecke oder Tetraedern) oder Finite Differenzen (also Rastern) zu rechnen.
Allerdings sind wir schon früh auf Rechenkästchen getrimmt worden, denken oft 2-dimensional in tabellenartigen Strukturen. Vielleicht liegt ist das Orthogonal für uns Normalsterbliche einfacher zu verstehen.
Pingback: Hexagone, die 2. | geoObserver
Pingback: ESRI meldet: “Hexagons are cool” | geoObserver
Pingback: Open Data Halle: Neue Themen | #geoObserver
Pingback: Warum man keine Postleitzahlen für räumliche Analysen verwenden sollte | #geoObserver