Vorletzte Woche konnte ich an einem Webinar von @cartocalypse teilnehmen. Ein Übungsbeispiel war die Kompaktheit von Geometrien. Dadurch angepingt wollte ich es genauer wissen und hab mal recherchiert. In „measuring-compactness-in-python“ [1] habe ich die entsprechenden Formeln für Kompaktheit nach Polsby-Popper [2] und Schwartzberg [3] gefunden:
def pp_compactness(geom): # Polsby-Popper
p = geom.length
a = geom.area
return (4*pi*a)/(p*p)def s_compactness(geom): # Schwartzberg
p = geom.length
a = geom.area
return 1/(p/(2*pi*sqrt(a/pi)))
Ich habe beide Formeln mal im QGIS mit dem Feldrechner eingefügt, einfach als virtuelle Felder mit „cpp“ für Polsby-Popper und „cs“ für Schwartzberg:
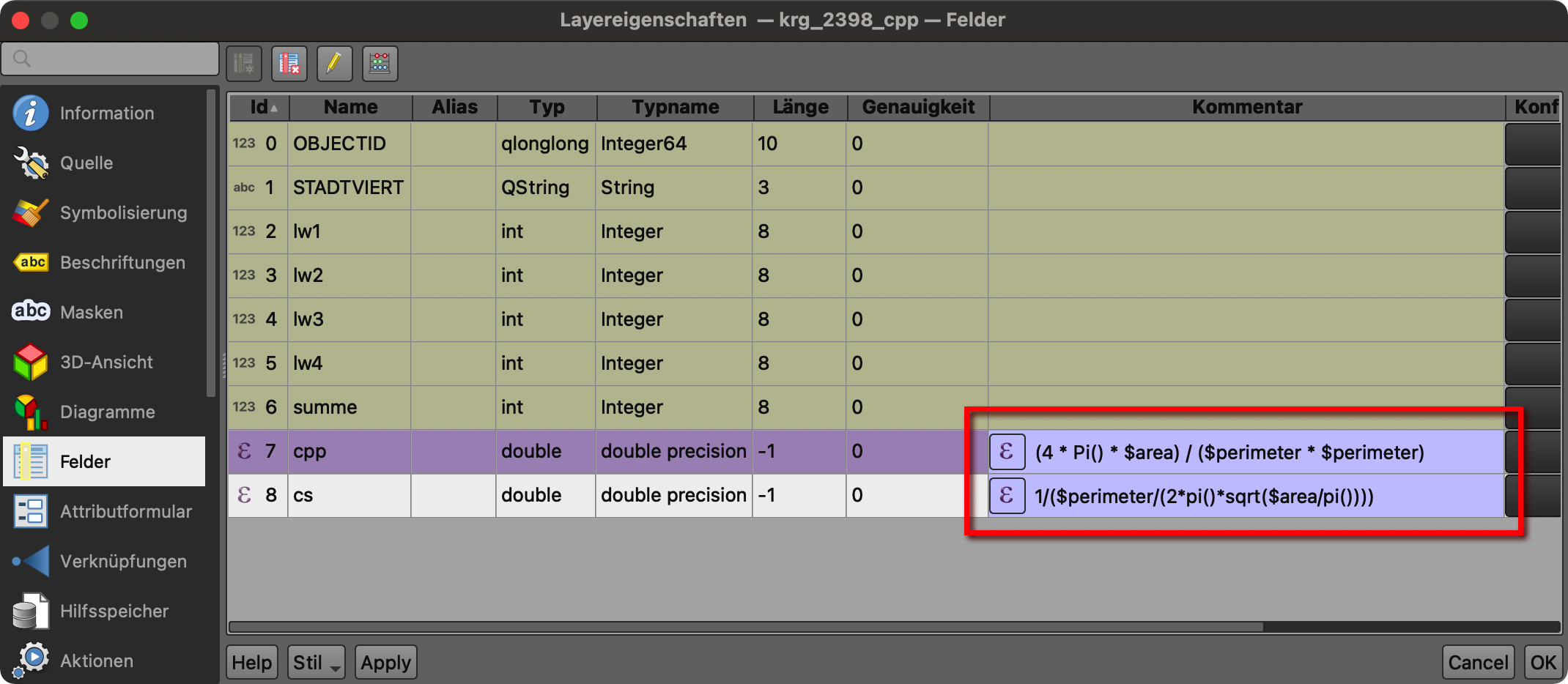
Hier die Ergebnisse visualisiert mit QGIS:
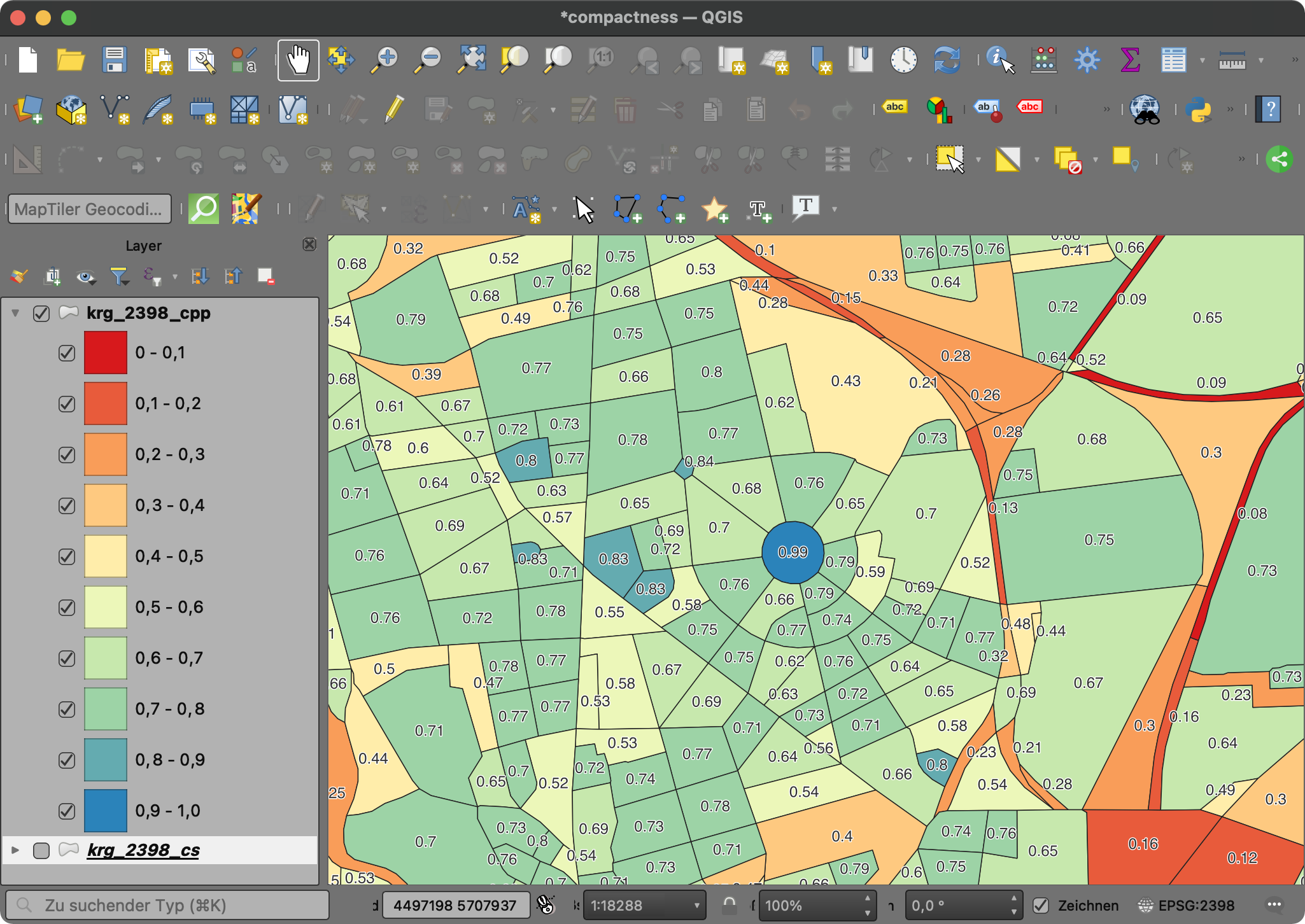
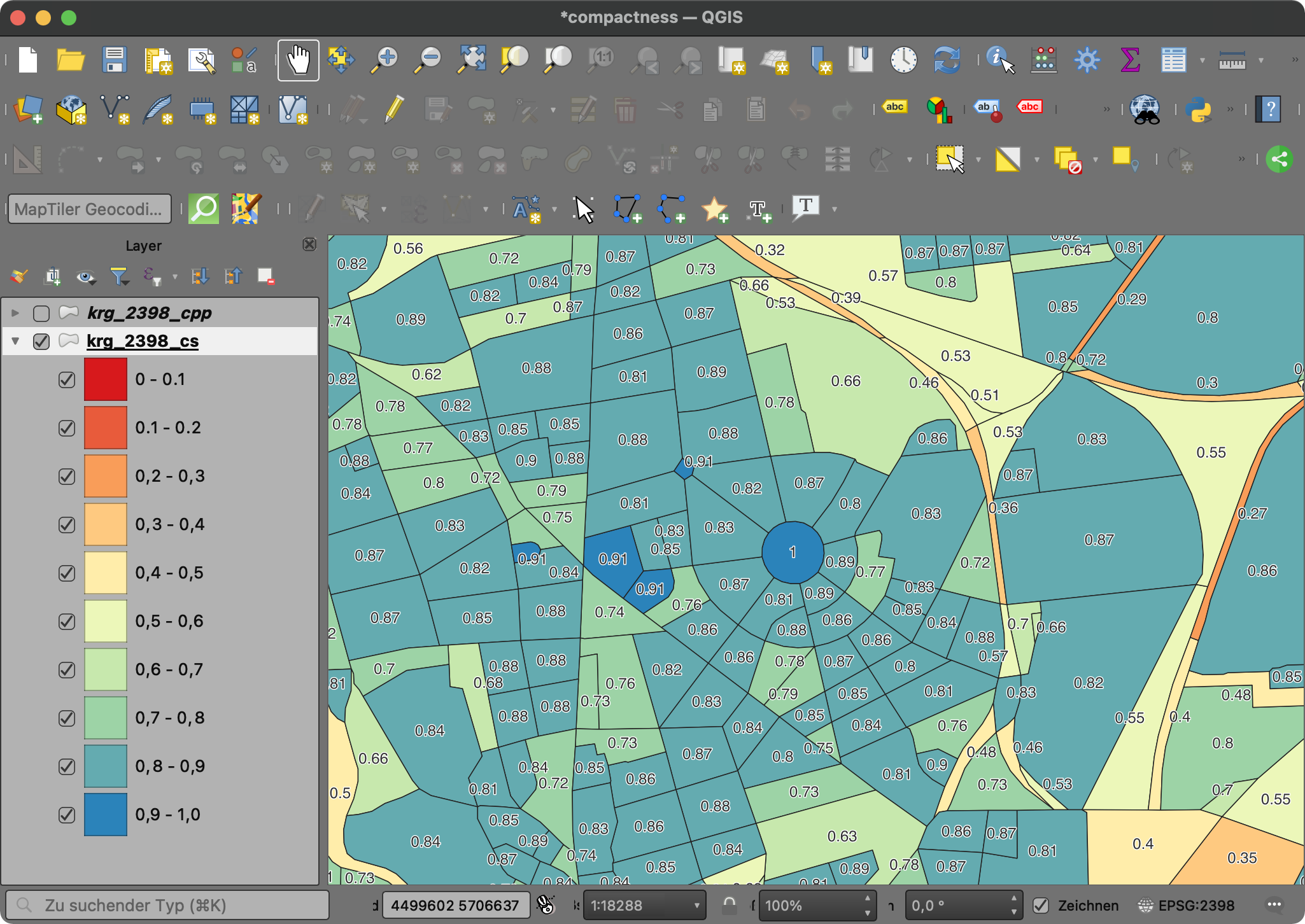
Und wer noch mehr über beide Verfahren wissen möchte, ich bin fündig geworden auf GitH^ub [4] mit „Compactness: Polsby-Popper vs. Schwartzberg“ auf Youtube [5]:
[1] … https://gis.stackexchange.com/questions/374364/measuring-compactness-in-python
[2] … https://en.wikipedia.org/wiki/Polsby%E2%80%93Popper_test
[3] … https://scholarship.law.umn.edu/cgi/viewcontent.cgi?article=2700&context=mlr
[4] … https://fisherzachary.github.io/public/r-output.html
[5] … https://www.youtube.com/watch?v=6Z_fuedTt4U

Pingback: QGIS: Die Kompaktheit von Polygonen | All Around GIS
Danke für die Kompaktheitsformeln und den Link zum Video!
In Qgis 3.24 wurde übrigens die roundness()-Funktion eingeführt, die die Polsby-Popper-Kompaktheit berechnet.