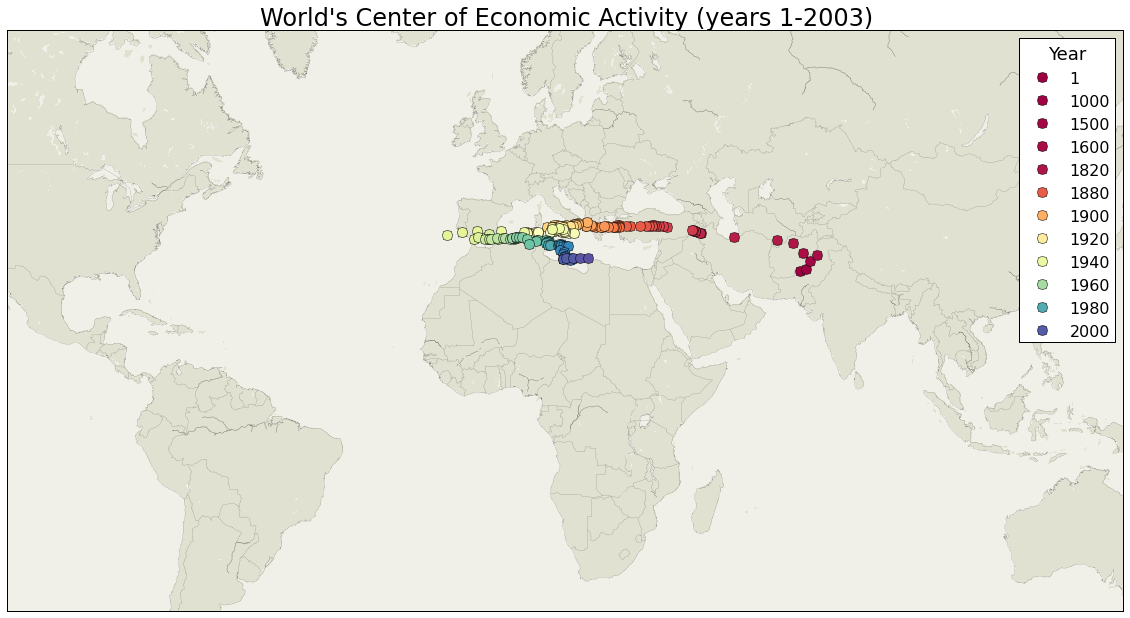
Der über die Zeit wandernde Schwerpunkt der Weltwirtschaft dargestellt auf einer Karte. Hochinteressant. Die Theorie dazu findet Ihr im Artikel „Die Suche nach der …“ mit einem bemerkenswerten Untertitel. Viel Spaß!
Gestern 23:31 kam die Nachricht via Twitter: Mapillary, das freie StreetView hat die
2-Millionen-Bilder-Grenze geschafft. Herzlichen Glückwunsch!
Am 23. Juli 1972 – da wechselte ich gerade in die 3. Klasse – startete der 1. Landsat-Satellit. Heute vor 42 Jahren. Herzlichen Glückwunsch auch vom geoObserver!
Schaut Euch einfach das folgende Video an NASA | Landsat’s Global Perspective, leider nicht nur schöne, beeindruckende, sondern sehr ernst zu nehmende Bilder!
Ohne Worte … Leider.
Quelle: https://de.wordpress.com/post/37597693/2755/
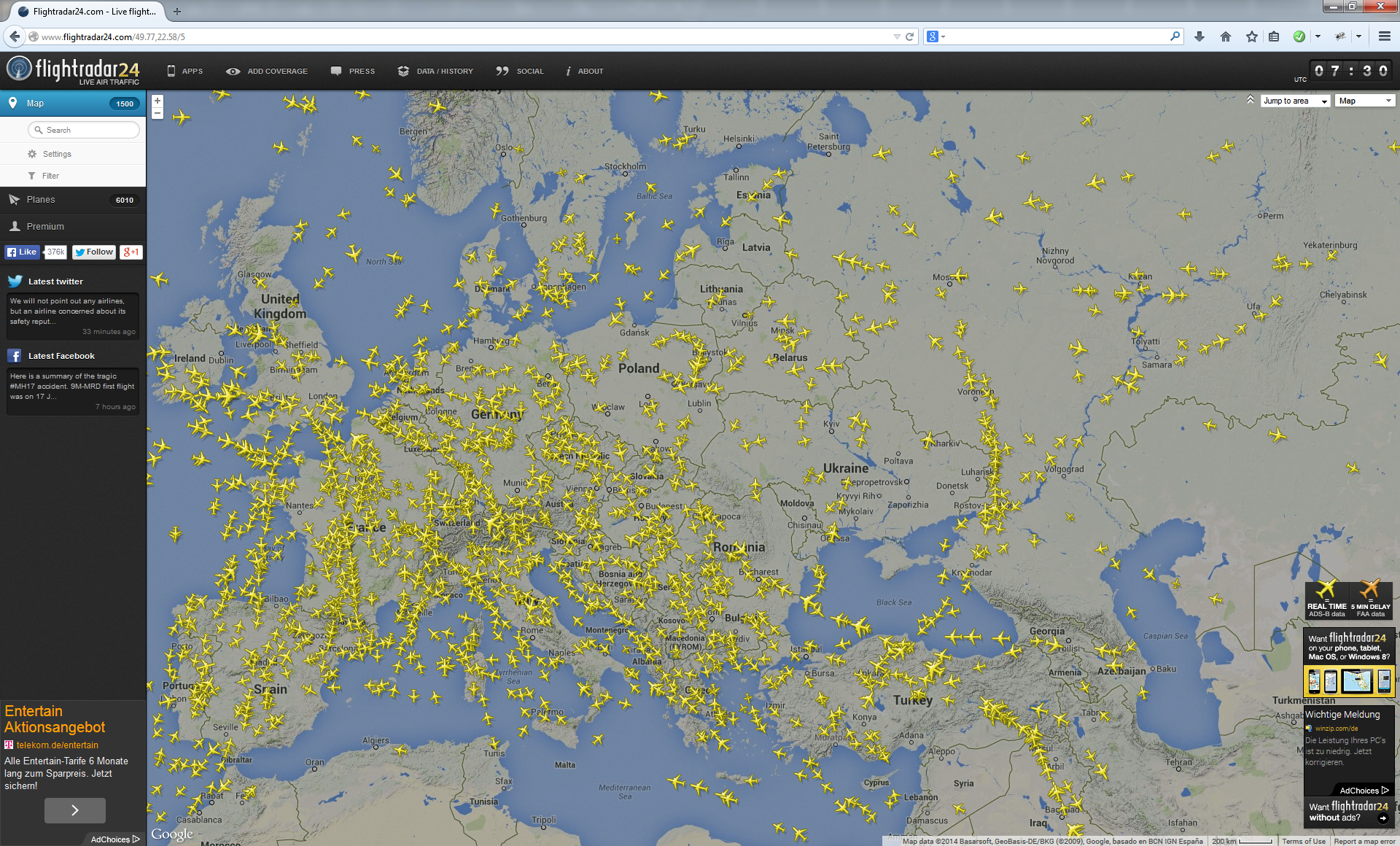
17.07.2014, 09:30 Uhr (MESZ)
Quelle: http://www.flightradar24.com/49.77,22.58/5
Mehr Infos unter: http://www.itc-halle.de/de/Service/Veranstaltungen/?EventID=81
Eine interessante Lösung – Daten und Anwendung – stellt die NOAA zur Verfügung. Hurricane-Daten von 150 Jahren können in einer interaktiven Karte nach Ort und Zeit selektiert und zur Anzeige gebracht werden.
Die fast aktuelle Karte der Fussballweltmeister finde Ihr beim LandkartenBLOG. Aber sie ist seit ca. 8 h nicht ganz aktuell, Deutschland hat ein Zähler/Stern mehr!
Und passend dazu heute die OSM-Buildings mal in SchwarzRotGold 😉
Auf diesem Weg noch mal allen Beteiligten ein herzliches Dankeschön für die Aufmerksamkeit und die Fragen und interessanten Fachdiskussionen danach beim Grillen. Danke für die Einladung, gerne wieder.
http://mars.geographie.uni-halle.de/geovlexcms/content/vortrag-mike-elstermann
Leider hab ich gestern das Webinar verpasst, aber Michael Hunger hilft auch hier und hat das Video vom Webinar online gestellt. Danke dafür – ich bin gespannt!
[vimeo 100456091 w=500 h=281]
Quelle: http://www.neotechnology.com/0710-einfuhrung-in-neo4j/
Unvorstellbar, schrecklich und doch faszinierend, die Darstellung der Wellenhöhen des 2011er Tsunamis in Japan verteilt über den gesamten pazifischen Raum:
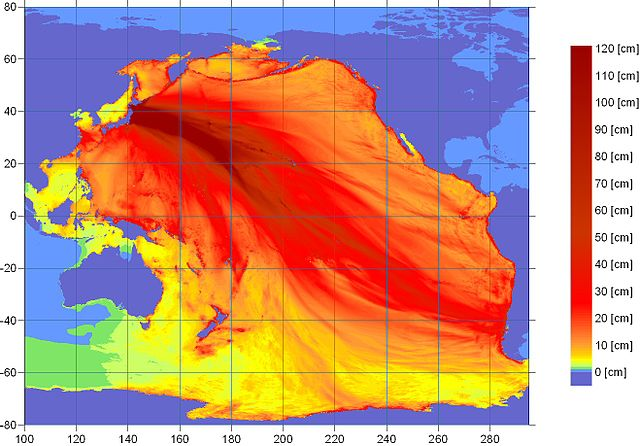
Quelle:
http://mapsontheweb.zoom-maps.com/image/90658932810
http://mapsontheweb.zoom-maps.com/post/90658932810/effect-of-the-2011-japanese-tsunami-throughout-the
